Option Greeks Calculator: Delta, Gamma, Theta, and Vega

This options calculator for the Greeks assumes the Black-Scholes model for calculating option Greeks and theoretical values. The results are purely hypothetical and based on user-provided data, including the risk-free rate, volatility, and time to option expiration.

What are Greeks in Options Trading?

The Greeks are a series of risk metrics that measure an option’s sensitivity to different factors. The most important thing to know about the Greeks is that they are forward-looking and provide insights into theoretical price movements under various scenarios.

Why are the Greeks Important?

The Greeks matter to options traders because they quantify how an option’s value reacts to changes in price, time decay, volatility, and even interest rates. They help traders determine whether an option is trading above or below its fair value prices under current market conditions.

For example, if you’re short a call option, wouldn’t it be helpful to know how that option’s value might change if implied volatility suddenly doubles? Or how the simple passage of time impacts your options? 

These questions are answered, respectively, by the Greeks vega and theta. Let’s take a closer look at the four primary Greeks.

Option Greeks Overview

Let’s start with a simple definition of each of the primary options Greeks, and then explore them one by one. 

• Delta: Measures how much an option's price is expected to change based on a $1 move in the underlying asset.
• Gamma: Tracks the rate of change in Delta as the underlying price changes.
• Theta: Represents the effect of time decay on an option's value.
• Vega: Gauges how sensitive an option’s price is to changes in implied volatility.‍
• Rho: Measures how much an option's price is expected to change based on a 1% change in the risk-free interest rate.

What is the Option Greek Delta?

The first and most widely cited Greek is delta. Delta measures how the value of an option will change for every $1 move (up or down) in the underlying asset—whether it’s a stock, index, ETF, commodity, or currency. 

Understanding delta is essential for anyone trading options. It would be nearly impossible to predict how an option’s price might react to future price movements without grasping how this fundamental Greek works.

In addition to measuring price sensitivity, delta also tells us:

• The probability that an option will expire in-the-money (ITM) at any given time.
• How many shares of stock an option trades like.

For example, a call option with a delta of 0.50 has a 50% chance of expiring ITM. This immediately indicates the option is at-the-money (ATM).

Additionally, because the delta is 0.50, the option behaves like 50 shares of stock. It’s important to note that this is a ballpark figure. Deep ITM options have a Delta approaching 1, meaning they trade similarly to 100 shares of stock.

Delta: Real World Example

Let’s take a look at a call options chain on SPY (SPDR S&P 500 ETF) on the TradingBlock dashboard and look at some live deltas.

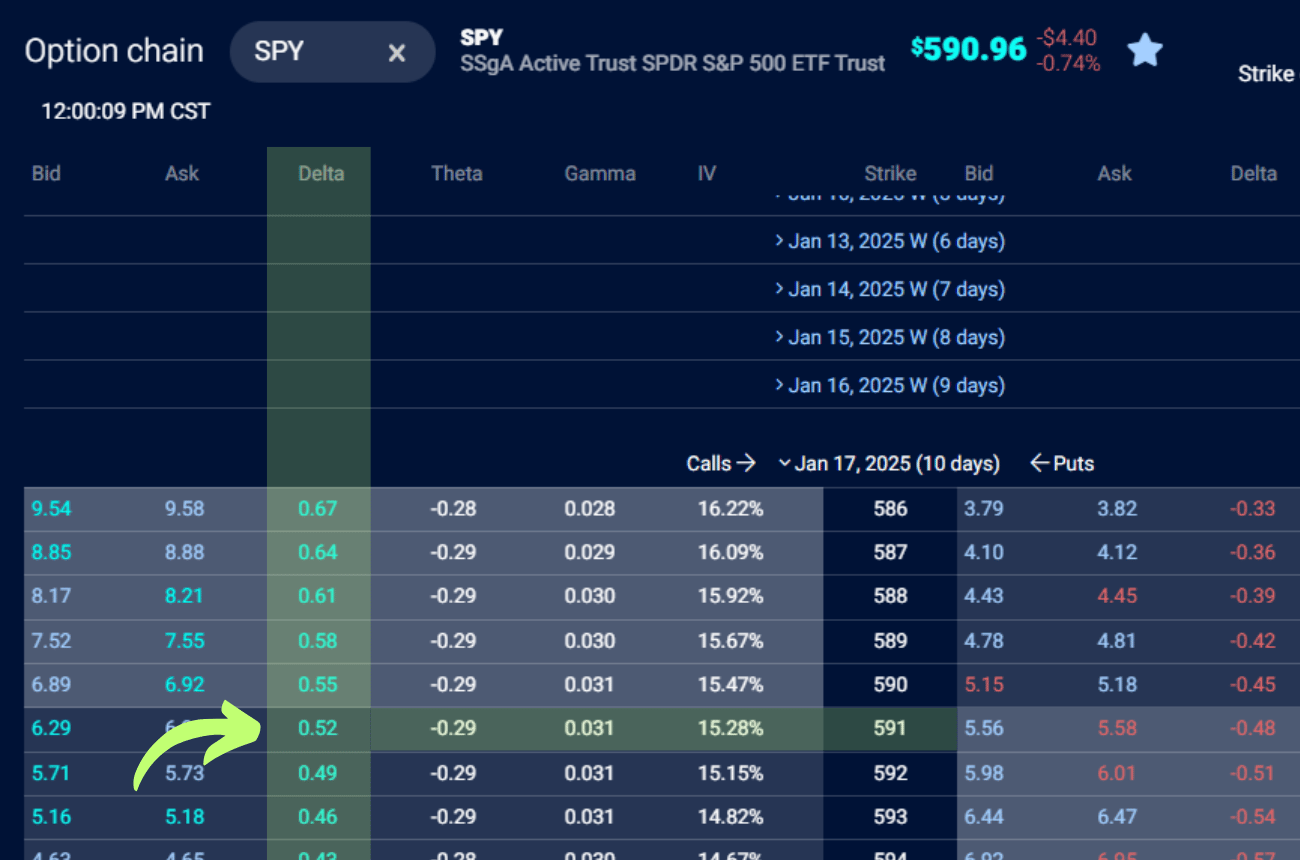
Here, we’re focusing on the $591 strike price call option, expiring in 9 days.

What This Tells Us:

We can see the Delta for this option is 0.52, or “fifty-two.” This tells us that for every $1 move up or down in the price of SPY, the option's value will rise or fall by $0.52.

Additionally, the 0.52 Delta tells us:

• The option has a 52% probability of expiring in the money (ITM).
• The option behaves like owning 52 shares of SPY in terms of price sensitivity

📖 Go In-Depth: Option Delta for Beginners

What is the Option Greek Gamma?

Delta measures how much an option's value changes in response to a stock price move, while gamma measures how quickly that change (delta) accelerates or slows down.

Gamma can be thought of as the delta of the delta. In other words, gamma measures how much delta will adjust for every $1 move in the underlying asset. Gamma Ranges from 0 to 1, and is highest for ATM options.

I like to think of gamma as the horsepower of an option. The higher the gamma, the more power the option has to accelerate changes in its price—either up or down.

Gamma is especially important for at-the-money (ATM) options, where it is highest. We can see this in the below visual comparing delta with gamma.

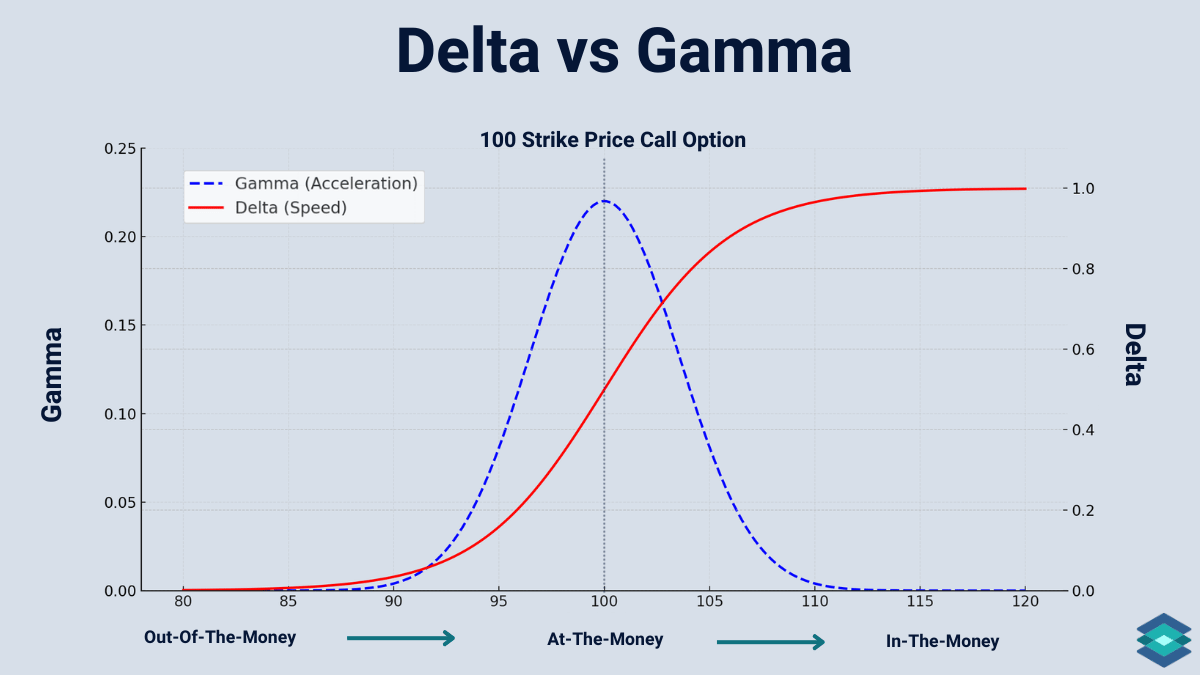
Notice that gamma decreases for deep in-the-money (ITM) and out-of-the-money (OTM) options as their delta becomes more stable and predictable.

Gamma: Real World Example

In this example, we’re analyzing the Gamma of a QQQ (Invesco QQQ Trust) put option on the TradingBlock dashboard. Specifically, we’re focusing on the $520 strike price put option, expiring in 6 days.

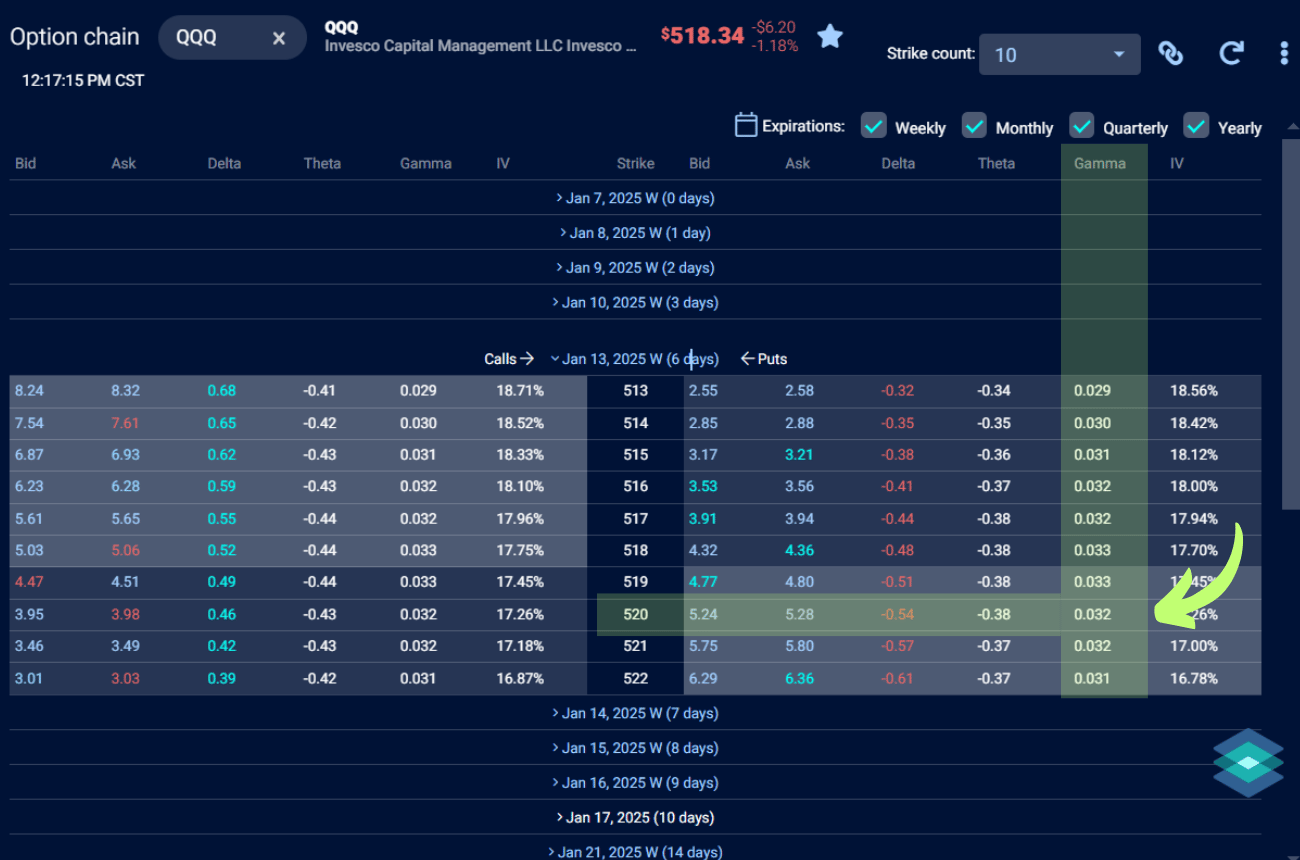
The gamma for this option is 0.032. 

What This Tells Us:

• For every $1 move in the price of QQQ, the delta of this put option will change by 0.032.
• If QQQ drops by $1, the delta of this put will become more negative, increasing its sensitivity to further price declines. Conversely, if QQQ rises by $1, the delta will become less negative, reducing its sensitivity to upward price movements.

📖 Go In-Depth: Option Gamma for Beginners

What is the Option Greek Theta?

The next Greek on our list deals with something all beginner option traders experience the hard way: time decay.

Unlike stocks, options are derivatives. This means they don’t trade forever—they have an expiration date. As time passes, if an option stays out of the money, the chance of it expiring in the money gets smaller and smaller. This reduces the value of the option. 

How Theta Measures Time Decay

The Greek theta tells us how fast the price of an option decays over time, assuming all other variables—such as the underlying price and implied volatility—remain constant. 

Theta is measured on a daily basis, meaning it shows how much extrinsic value an option loses each day as time passes. For example, if an option has a theta of -0.05, the option’s price will decrease by $0.05 every day, all else being equal.

What’s interesting about theta is that it accelerates as expiration approaches—it’s not linear. We can see this below:

Theta: Real World Example

Let’s jump back over to the TradingBlock platform for a real-work example. 

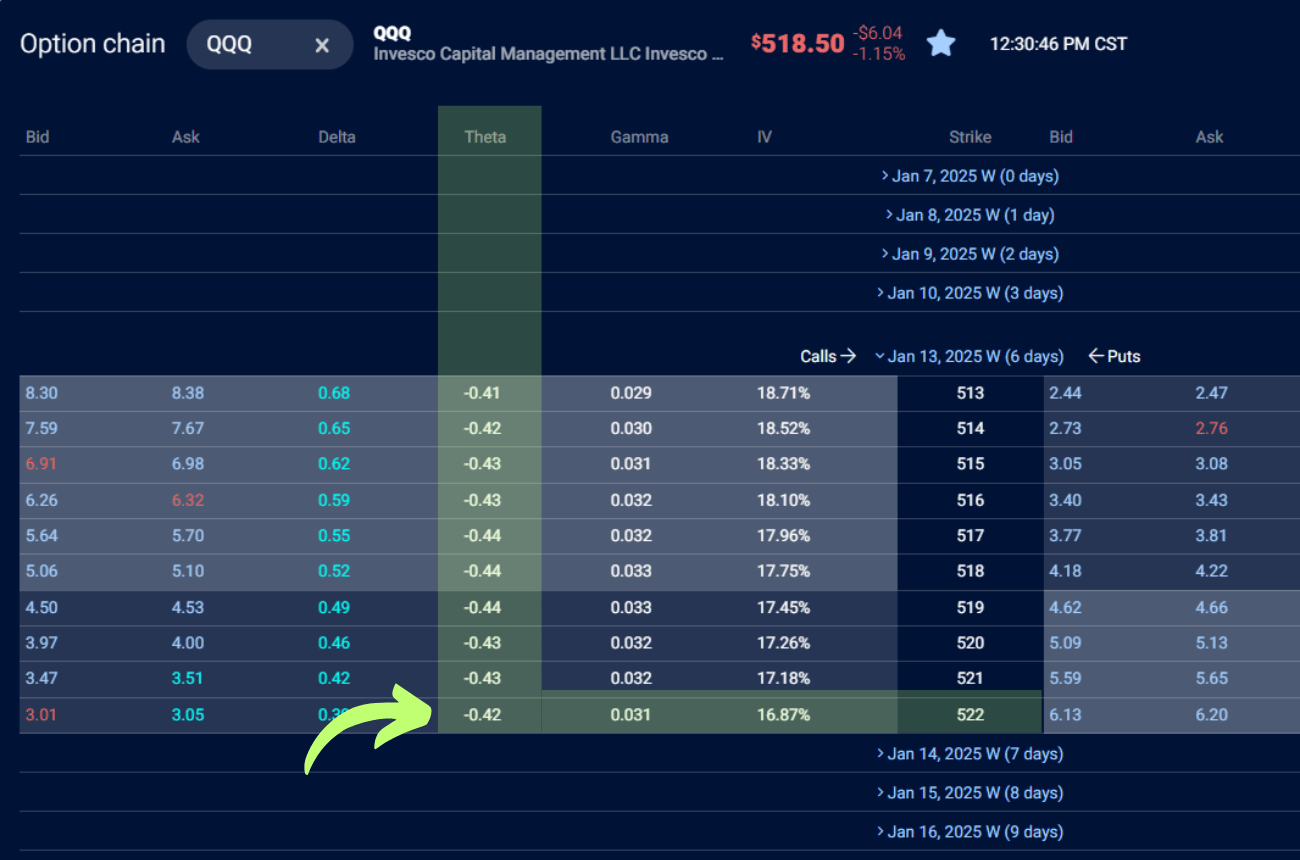
Here, we are looking at the various thetas for call options on QQQ , expiring in 6 days, specifically the $522 strike price call option, which has a theta of -0.42.

What This Tells Us:

• The Theta of -0.42 means that this option will lose $0.42 in value per day as time passes, assuming the underlying price and implied volatility remain constant.
• As expiration approaches, the impact of theta accelerates, meaning the option's value will decay faster each day if it remains out of the money.

Theta is negative for all long options and typically ranges from -0.01 to -1.00.

What is the Option Greek Vega?

The option Greek vega measures an option's sensitivity to changes in implied volatility (IV). 

Unlike the other Greeks we’ve covered, vega does not directly relate to the underlying asset's price movement. Instead, it focuses on how fluctuations in market expectations of volatility impact an option's value.

Rising IV is like a tide that raises all ships. When IV increases, the value of both call options and put options rises. This benefits option buyers, as higher IV makes options more expensive.

On the other hand, when IV falls, the price of all options decreases, which works in favor of option sellers who profit from declining option premiums.

Vega: Trade Example

For example, a call option with a vega of 0.12 implies that for every 1% increase in IV, the option’s price will increase by $0.12. Conversely, if IV drops by 1%, the option’s price will decrease by $0.12.

What is the Option Greek Rho?

The option Greek rho measures an option’s sensitivity to changes in interest rates. Specifically, rho tells us how much the price of an option will change for a 1% change in the risk-free interest rate.

Professionals mostly use this Greek, as interest rates tend to have a smaller impact on options pricing than other factors like volatility or time decay. However, Rho becomes more significant for options dated far in the future, such as LEAPS. 

Rho: Trade Example

For example, a call option with a rho of 0.10 means that for every 1% increase in interest rates, the option’s price will increase by $0.10. Conversely, if interest rates decrease by 1%, the option’s price will decrease by $0.10.

Calculating the Greeks

For those who want to get into the weeds with the option Greeks, here are the calculations used to calculate each one for both option types. We’ll start with the variables used: 

Variables:

• S = Current stock price
• K = Strike price
• T = Time to expiration (in years)
• r = Risk free rate
• σ = Volatility of the underlying asset
• N(d) = Cumulative distribution function (CDF) of the standard normal distribution
• N'(d) = Probability density function (PDF) of the standard normal distribution
  

Option Delta Calculation

For Call Options:
Delta = N(d1)

For Put Options:
Delta = N(d1) - 1

d1 = [ln(S/K) + (r + σ²/2) * T] / (σ * √T)

Option Gamma Calculation

Gamma = N'(d1) / (S * σ * √T)

Option Theta Calculation

For Call Options:
Theta = [-S * N'(d1) * σ / (2 * √T)] - [r * K * e^(-rT) * N(d2)]

For Put Options:
Theta = [-S * N'(d1) * σ / (2 * √T)] + [r * K * e^(-rT) * N(-d2)]

d2 = d1 - σ * √T

Option Vega Calculation

Vega = S * N'(d1) * √T

Option Rho Calculation

For Call Options:

Rho = K * T * e^(-rT) * N(d2)

For Put Options:‍

Rho = -K * T * e^(-rT) * N(-d2)
‍

‍

⚠️ Disclaimer: When using the Option Greeks Calculator, remember that it provides hypothetical values based on the Black-Scholes model and specific input parameters. It does not account for commissions, fees, or other transaction costs, which can significantly impact your net profit or loss. This tool is for informational purposes only and should not be relied upon as the sole basis for investment decisions. Always factor in costs such as commissions when planning your trades. Be sure to read Characteristics and Risks of Standardized Options before trading options.