Option Rho Explained: The Greeks for Beginners

RHO and the Greeks

In options trading, the Greeks are a set of risk metrics that help gauge how the price of an options contract might react under different scenarios. The most common Greeks include:

• Delta: Measures how much an option's price is expected to change for a $1 move in the underlying asset.
• Gamma: Measures the rate of change in delta as the underlying asset moves.
• Theta: Reflects the impact of time decay, showing how much an option's price decreases as time passes.
• Vega: Indicates how much an option's price will change with a 1% shift in implied volatility.

Then there's rho, which measures how sensitive an option's price is to changes in the risk-free interest rate.

Rho is often the most neglected of the Greeks because changes in interest rates tend to have a smaller immediate impact on option prices compared to factors like volatility or the underlying asset's price movements. However, rho becomes more significant for longer-dated options and in markets where interest rates change rapidly. 

When interest rates rise, call options generally increase in value, while put options decrease in value, with all else being equal.

📊 Check Out Our Option Greeks Calculator Here!

What Is the Risk-Free Rate?

In investing, “interest rates” are synonymous with the risk-free rate. While often derived from Treasury yields, there’s no single risk-free rate - traders may reference different maturities depending on the context, like short-term T-bills or longer-term notes.

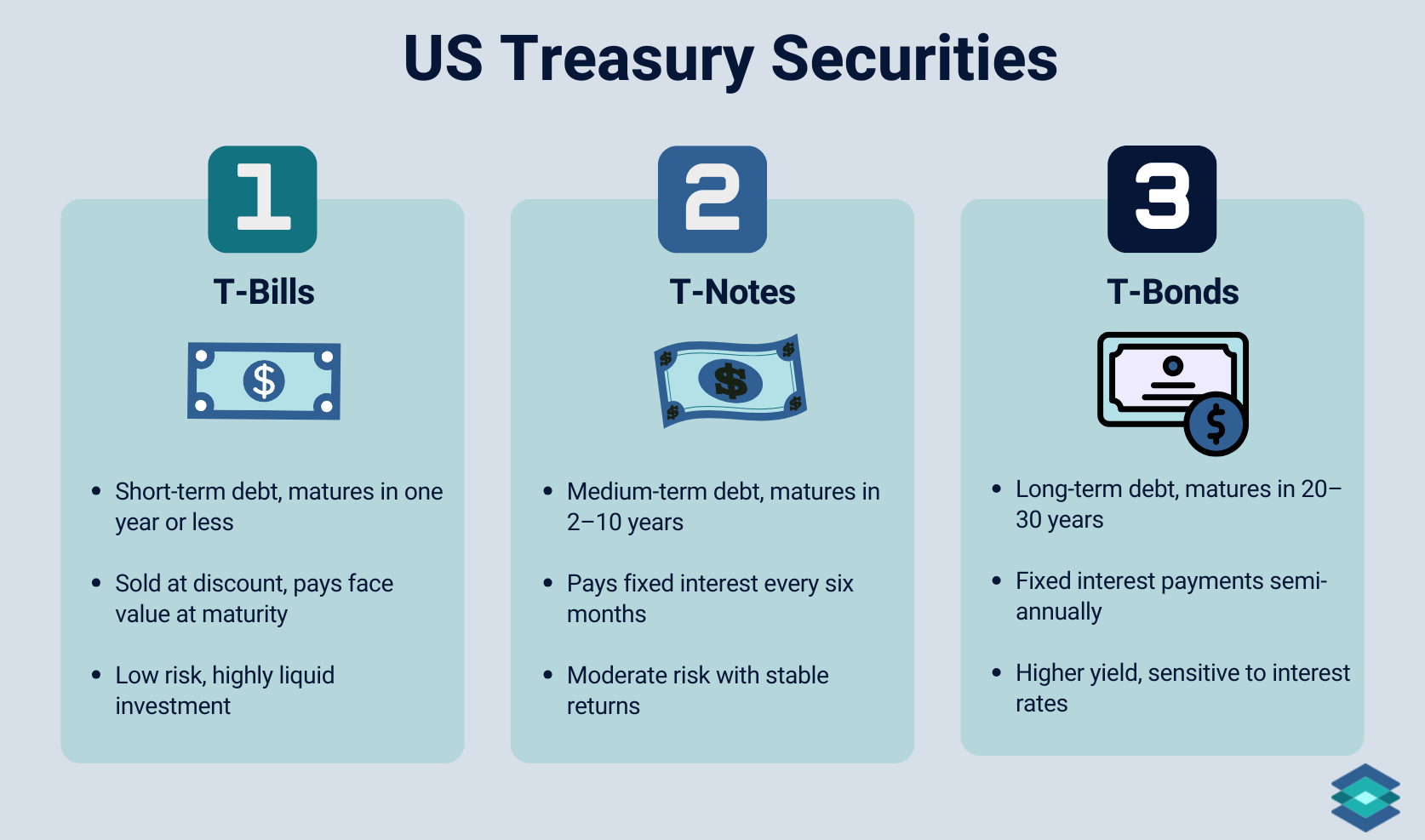
While treasury securities are often seen as risk-free, they’re not entirely without risk—just as close to risk-free as it gets. Traders use these rates to gauge the return they could earn by doing nothing. They also represent an opportunity cost—the potential return you give up by investing your capital elsewhere

Now that we’ve covered the basics, let’s see how this plays out with a real trade scenario.

Risk-Free Rate Example

Let’s say you decide to sell an out-of-the-money call option on SPY (SPDR S&P 500 ETF Trust) expiring in 6 months for a premium of $2. Here are our trade details:

• Selling a Call Option on SPY:
  
  • You sell a call option on SPY that expires in 6 months for a premium of $200 (assuming a premium of $2 per share for 100 shares).
  • The margin requirement for this trade is $9,800.
  • This brings your total capital tied up to $10,000 (premium received + margin requirement).
  • After 6 months, the call expires worthless.
  • Your total return: $200, which represents a 2.04% return on the $9,800 held as margin (which earns no interest during that period).
    
    

Now, what if you instead invested that $10,000 into T-bills?

• Investing in a Treasury Bill (T-bill):
  
  • You invest $10,000 in a T-bill for 6 months.
  • At today's risk-free rate (as of February 2025), you earn $215.18.
  • Your total return: $215.18 (2.15% return on your $10,000 investment), with no risk involved.

Since T-bills are considered “risk-free” and selling a naked call option involves significant risk and ties up margin that earns no interest, it’s clear what the better trade is. 

How Does Rho Work?

Rho measures the sensitivity of an option’s price to changes in the risk-free interest rate. It tells you how much the price of an option will increase or decrease with a 1% change in interest rates, assuming all other factors remain the same.

Rho typically ranges between -1 and 1 for standard options, though it can be higher or lower depending on the option's specifics.

• Call options have positive Rho, meaning their value increases with interest rates.
• Put options have negative Rho, meaning their value decreases as interest rates rise.

Rho tends to be small and less impactful for most short-term options, while longer-dated options (like LEAPS) show a more pronounced rho effect.

Rho: Options Chain Example

Let’s look at a real-world options chain on SPY (SPDR S&P 500 ETF Trust) to see rho in action. Remember that call options are always on the left side of an options chain, while put options are on the right.

Take the 604 strike price call option as an example. The rho on this call is currently 0.32. This means that if interest rates increase by 1%, the price of this call option will rise by 0.32. Conversely, if interest rates were to decrease by 1%, the price of this call option would fall by 0.32.

For put options, the rho values are negative, meaning that as interest rates rise, the price of a put option tends to decrease.

Rho and Time to Expiration

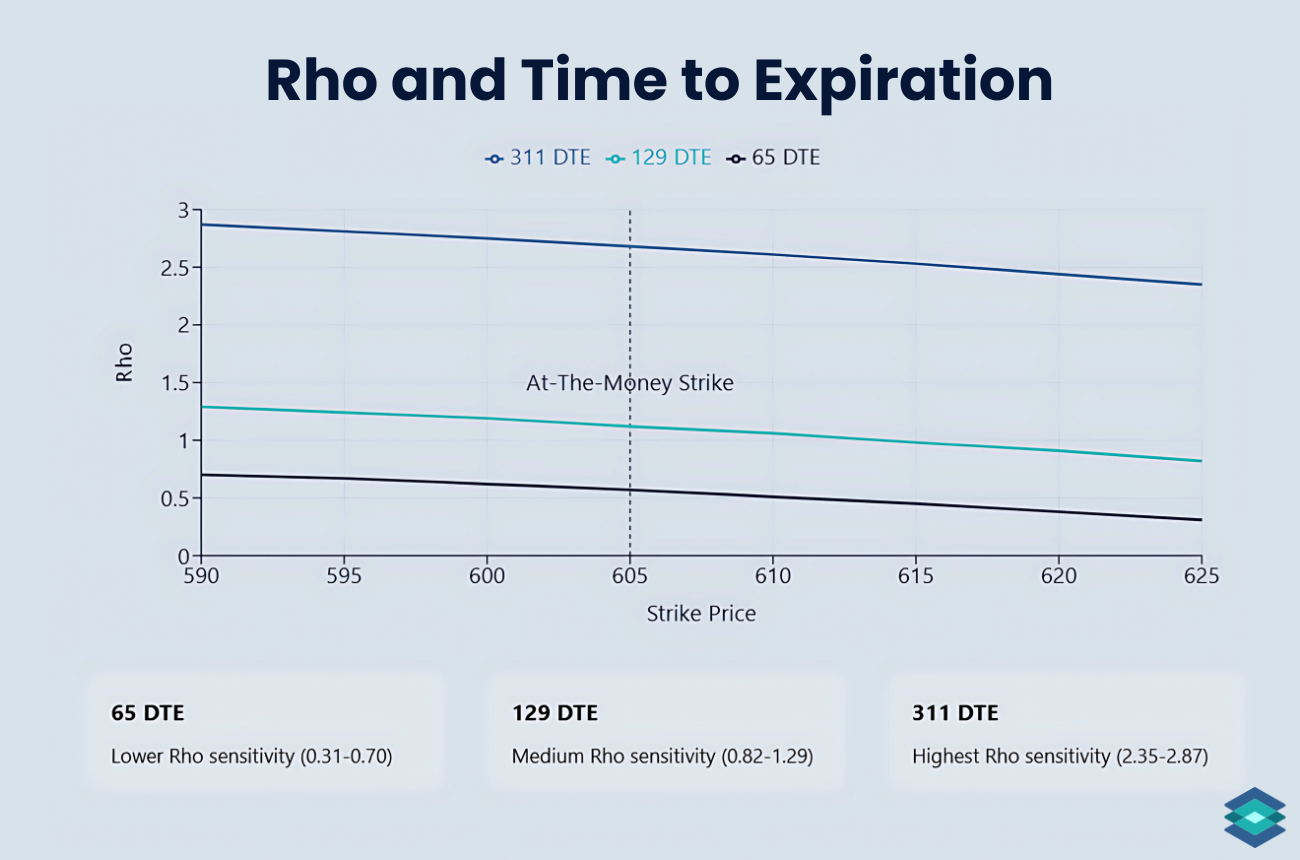
The above chart shows three different option expiration cycles for SPY (SPDR S&P 500 ETF Trust) call options: 65, 129, and 311 days until expiration (DTE). The rho values were taken in real-time. 

As expiration cycles lengthen, the sensitivity of options to interest rate changes grows greater. As we can see, the 311 DTE options exhibit the highest rho sensitivity, while the 65 DTE options demonstrate the lowest. 

This confirms that longer-dated options are more affected by interest rate fluctuations due to their extended time until expiration, offering more time for the underlying price and interest rates to influence the option's value.

Moneyness and Rho

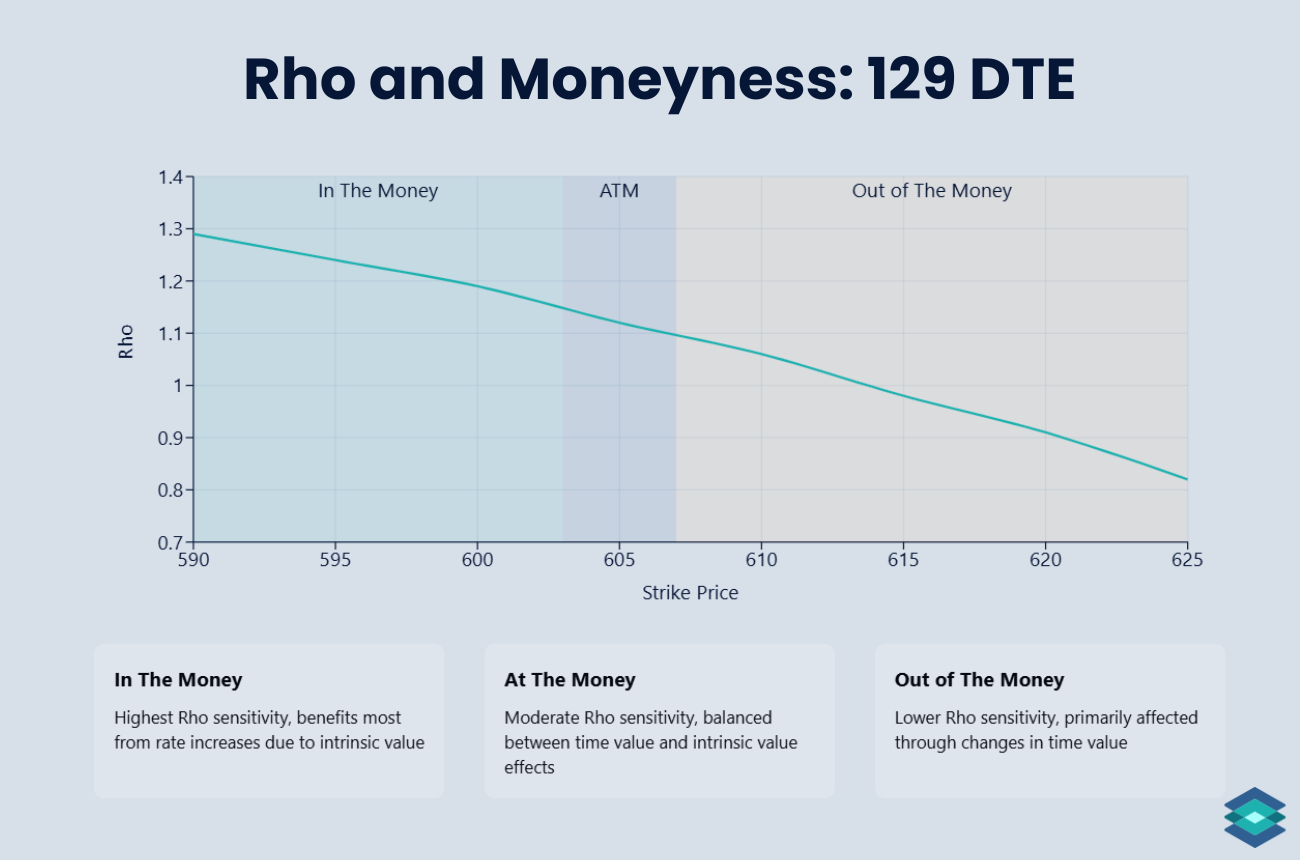
The above graph shows rho values for various SPY long call options strike prices. Note how the rho value of any option is contingent upon that option’s moneyness:

• In-the-Money (ITM) Options: Higher rho due to significant intrinsic value, making them more sensitive to interest rate changes.
• At-the-Money (ATM) Options: Moderate rho sensitivity as both intrinsic and time value balance the impact of interest rates.
• Out-of-the-Money (OTM) Options: Low rho sensitivity since minimal intrinsic value limits the effect of interest rate changes.

This tells us that the higher an option's intrinsic value is, the more it will react to changes in interest rates.

Option Rho Formula

For all you math geeks out there, here are the formulas you can use to calculate rho on your own for both calls and puts: 

Call Option Rho Calculation:

ρ=K⋅t⋅e−rt⋅N(d2​)

Put Option Rho Calculation:

ρ​=−K⋅t⋅e−rt⋅N(−d2​)

Variables:

• K = Strike Price
• t = Time to Expiration
• e^(-r*t) = Exponential Discount Factor
• N(d₂) = Cumulative Distribution Function (CDF) of the Standard Normal Distribution
  ‍

⚠️ The examples provided in this article are for illustrative purposes only and do not include commissions, fees, or other transaction costs. These costs should be factored into all trading decisions, as they can impact the overall profitability of a trade. Always understand the risks associated with investing and read The Characteristics and Risks of Standardized Options before trading options.